THE WIGNER-POISSON SYSTEM
General Considerations
We study the quantum analogue of the classical
steady-state solutions of the Vlasov-Poisson system (BGK modes), introduced by
Bernstein, Greene and Kruskal in 1957 and
describing the spatially inhomogeneous equilibria of a collisionless
unmagnetized plasma with immobile ions. The quantum version
of the Vlasov-Poisson system is the Wigner-Poisson system, in which
the Wigner distribution takes the place of the
classical distribution function and obeys an evolution equation where
the acceleration term is given by a pseudo-differential operator, in
place of the usual differential operator of the Boltzmann equation. The steady-state
Wigner-Poisson system admits spatially
periodic solutions. Furthermore, it is well known that the Wigner-Poisson system
reduces to the Vlasov-Poisson system in the classical limit.
It is therefore natural to look for small quantum corrections to the
classical BGK equilibria by using perturbation methods.
Results
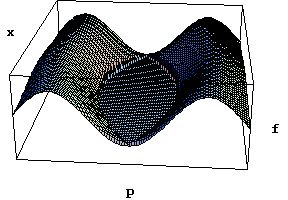
In (1), we develop a first-order perturbation
theory and produce numerical results
showing the quantum corrections to the classical BGK equilibria generated by a
two-stream distribution. The
results show that the quantum correction to the BGK potential
amounts to a
decrease of the amplitude and a shortening of the period and
that the differences between the classical distribution
function and the Wigner function, as determined by our
first-order perturbative expansion, are most evident near the separatrices.
-
L. Demeio, Perturbative approach to Quantum
BGK Modes, Proc. VI
Congresso Nazionale SIMAI, Chia Laguna (CA-Italy) May 27-31, 2002.

