Calcolare
con il DNA
Raffaella Franci *
In memoria di
Alberto Del Lungo
(1965-2003)
amico e collega
indimenticabile.
Il computer elettronico è forse il prodotto più
popolare e di più ampio impatto
sociale e culturale dello sviluppo tecnologico e scientifico del XX secolo. Nel
1951 quando veniva terminato e prodotto in sette esemplari il primo UNIVAC (
Universal Automatic Computer), il calcolatore elettronico usciva dall’ambito
militare e diventava un prodotto commerciale ad uso civile. L’evoluzione di
questo manufatto è stata sorprendente; mentre le dimensioni diminuivano, la
potenza di calcolo aumentava a livelli che all’inizio sarebbero stati
inimmaginabili.
Per
ottenere l’aumento delle prestazioni si ricorre in modo massiccio alla
miniaturizzazione dei componenti, che però ha un suo limite fisico: non si può
andare sotto le dimensioni atomiche. Secondo la cosiddetta Legge di Moore[1],
questo limite sarà raggiunto nel 2014. A questo punto se si desiderano
calcolatori più potenti bisogna cambiare radicalmente tecnica. Vari gruppi di
ricercatori sono al lavoro da tempo e si stanno profilando almeno due ipotesi
molto promettenti: i quantum-computer[2]
e i DNA-computer. Il
primo esemplare di questi ultimi è
stato realizzato da L.A. Adleman e descritto in un articolo pubblicato nel 1994
nella rivista Science, [1].
Leonard A. Adleman, matematico e informatico nonché
esperto di biologia molecolare, era all’epoca già molto noto per avere
elaborato assieme a R. Rivest, e A. Shamir il sistema di crittografia a chiave
pubblica maggiormente in uso oggi, il sistema RSA[3].
L’articolo di Adleman che descrive l’uso sperimentale
del DNA come sistema computazionale applicato alla risoluzione di un’istanza
del problema del cammino hamiltoniano per un grafo orientato, ebbe subito una
vastissima risonanza. Solo cinque mesi dopo in un congresso organizzato in gran
fretta alla Princeton University, al quale parteciparono circa duecento fra
informatici e biologi molecolari, furono descritti numerosi schemi per
applicare tecniche di biologia molecolare a problemi computazionali: dalla
decifrazione di codici alla costruzione di computer universali.
Era nata una nuova disciplina: il calcolo con il
DNA, che da allora ha avuto uno
sviluppo tale da rendere impossibile darne conto, anche in modo sommario, nel breve spazio di un articolo. Mi
limiterò pertanto a descrivere il calcolo eseguito da Adleman nel suo
pionieristico esperimento e quello successivamente proposto a livello teorico da
Lipton per verificare la soddisfacibilità di una formula booleana, nell’intento
di informare anche i non specialisti, alla schiera dei quali appartiene anche
chi scrive, di questo nuovo e interessante genere di calcolo.
1.
Il DNA ed alcune tecniche di biologia molecolare
Le informazioni che presiedono alla formazione e al
funzionamento degli organismi viventi, cioè il loro patrimonio genetico, sono
codificate nelle molecole di DNA contenute all’interno dei cromosomi presenti
nel nucleo di ogni cellula.
DNA è l’acronimo di DeoxyriboNucleic Acid (acido
deossiribonucleico). Si tratta di una macromolecola, cioè di una molecola
grande, o meglio lunga, makros in
greco significa, infatti, lungo. I suoi costituenti primari, i nucleotidi, sono formati da un fosfato, uno zucchero e una base
azotata. Mentre il legame zucchero-fosfato è sempre uguale, lo zucchero si lega
a quattro tipi diversi di basi: adenina, guanina, citosina e timina, che vengono comunemente indicate con le loro lettere
iniziali maiuscole A, G, C e T. I nomi delle basi sono generalmente usati anche per
riferirsi ai nucleotidi che le contengono.
Ogni molecola di DNA è formata da due filamenti
ciascuno dei quali è costituito da una successione anche molto numerosa di
nucleotidi. Gli zuccheri sono disposti a uguale distanza sul bordo, mentre le
basi si protendono e si legano a quelle dell’altro filamento con un legame
idrogeno piuttosto debole rispetto agli altri. Gli unici legami possibili fra
le basi sono adenina con timina, A=T (due legami idrogeno), e guanina con
citosina, G≡ C (tre legami idrogeno).
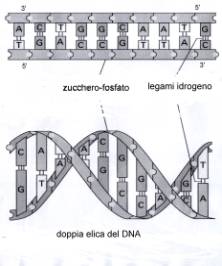
Fig. 1-
Filamento doppio di DNA
I due filamenti di una molecola di DNA risultano
quindi complementari rispetto a questi legami, per convenzione l’estremità di
un filamento è chiamata 3’, mentre l’altra è denominata 5’. I filamenti
complementari sono antiparalleli, nel senso che l’estremità 3’ di uno di essi
si appaia con l’estremità 5’ dell’altro e viceversa; pertanto ognuno dei due
può fungere da stampo sul quale realizzare la catena complementare, Fig. 1. I
due filamenti formano nello spazio una doppia elica che si ripiega in modo così
compatto da entrare nel nucleo della cellula [4].
Le molecole di DNA pur essendo così complesse hanno
dimensioni assai ridotte. Per esempio una molecola di DNA umano, che contiene
circa tre miliardi di basi, è lunga circa due metri e larga 10-6
millimetri. Dopo essersi avvolta ad elica e ripiegata entra nel nucleo che ha
un diametro di un centesimo di millimetro, Fig. 2 .
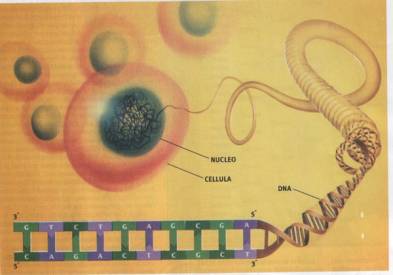
Fig. 2
La notorietà del DNA fuori della comunità scientifica
è dovuta in gran parte al progetto di sequenziamento del genoma umano,
largamente pubblicizzato dai mezzi di informazione per le sue importanti
ricadute nell’ambito della medicina[5].
L’attuazione del progetto, completato agli inizi del 2001, è stata più rapida
del previsto grazie anche alla messa a punto di nuove tecniche biologiche che
consentono di effettuare sorprendenti operazioni sulle molecole di DNA. Per
realizzare queste operazioni le molecole di DNA coinvolte vengono messe in soluzione
con acqua, zuccheri e talora particolari enzimi che ne facilitano l’esecuzione.
Qui di seguito elenchiamo solo quelle che sono coinvolte nei calcoli con il DNA da noi
presentati.
·
Separazione (melting): divisione di una molecola o di un
frammento di DNA nei due filamenti complementari che lo costituiscono. Si
ottiene riscaldando la soluzione, in tal caso infatti il debole legame idrogeno
che tiene insieme le coppie di basi complementari si spezza.
·
Accoppiamento (annealing): unione di due filamenti di DNA
complementari. Si ottiene raffreddando la soluzione, l’aggiunta dell’enzima ligasi rende più stabili gli accoppiamenti.
·
Amplificazione: produzione di copie di un filamento di DNA mediante
la reazione a catena
della polimerasi che permette di replicare
un filamento di DNA. La sua realizzazione è resa possibile da un enzima il DNA-polimerasi, che legge il filamento e sceglie da una miscela di
basi a sua disposizione quale inserire seguendo la legge di complementarietà.
La reazione è molto veloce e permette in poco tempo, di replicare un dato
filamento di DNA milioni di volte; essa, infatti, consiste nella ripetizione di
una serie di cicli in ciascuno dei quali il materiale raddoppia, per cui da un
singolo filamento di DNA dopo n cicli si hanno 2n copie.
·
Elettroforesi su
gel: è una tecnica che permette
di separare i filamenti di DNA per lunghezza. Per effettuarla una soluzione di
molecole di DNA di diversa lunghezza viene posto in un pozzetto all’estremità
di un sottile strato di gel a cui viena applicata una corrente elettrica. Le
molecole di DNA che hanno una carica elettrica negativa, vengono attirate verso
l’anodo, le molecole più corte migrano più velocemente di quelle più lunghe.
L’insieme di quelle che hanno la stessa lunghezza appaiono come bande a diversa
distanza dal pozzetto, Fig. 3. Si possono vedere utilizzando particolari
reagenti e illuminando il gel con luce ultravioletta, è altresì possibile con
una semplice tecnica calcolare esattamente il peso molecolare di ciascun
frammento separato.
·
Separazione o
estrazione per affinità: è una
tecnica che permette, sfruttando il principio di complementarietà delle
basi, di estrarre filamenti di DNA
aventi dei sottofilamenti con determinate configurazioni.
·
Sintesi
artificiale del DNA: è possibile
realizzare, in breve tempo e a costi contenuti, molecole di DNA aventi la
struttura desiderata, di lunghezza fino a 100 nucleotidi.
Fig. 3 Elettroforesi su gel
2. Il Problema del percorso hamiltoniano.
Un grafo orientato è un insieme di punti, detti vertici, uniti da un insieme di linee orientate, dette lati. Un cammino hamiltoniano su un grafo orientato è un percorso che inizia da un
vertice ed arriva ad un altro dopo essere passato per tutti i vertici
esattamente una volta. Se il grafo ha n vertici un tale cammino, se esiste, è formato da n-1
lati.
Il Problema del percorso hamiltoniano per un grafo
orientato (PPHO), chiede di stabilire
se in un dato grafo orientato in cui siano scelti due vertici, esiste almeno un
cammino hamiltoniano che li unisce.
La difficoltà di risoluzione del PPHO non è
concettuale, un modo per trovare la eventuale soluzione è, infatti, descritto
dal seguente semplice algoritmo.
Passo
1. Si generano tutti i cammini attraverso il grafo
Passo 2. Per ogni percorso si verifica se inizia nel vertice di partenza e termina in quello di arrivo. Se questo non succede si scarta il percorso.
Passo
3. Per ogni percorso si verifica se passa esattamente per n vertici. Se questo non succede si scarta il percorso.
Passo
4. Per ogni percorso e per ogni vertice si verifica se il percorso passa
per quel vertice. Se questo non succede si scarta il percorso.
Passo
5. Se non tutti i percorsi sono stati scartati registrare che esiste un
cammino hamiltoniano. Altrimenti registrare che non esiste.
Ovviamente
l’algoritmo in caso di risposta positiva fornisce anche gli eventuali cammini
hamiltoniani.
La difficoltà nella risoluzione di PPHO risiede nella
circostanza che l’algoritmo descritto, così come tutti gli altri attualmente
noti, richiedono nel caso di un numero relativamente grande di vertici un tempo
di esecuzione così lungo che non permette di trovare la soluzione neppure con
l’ausilio dei più potenti computer elettronici. Questo dipende dal fatto che il tempo di esecuzione
dell’algoritmo cresce esponenzialmente al crescere del numero n dei vertici del grafo.
Il PPHO è un esempio di problema NP-completo, cioè non
deterministico in tempo polinomiale. Una caratteristica di questi problemi è
che mentre è facile verificare che una soluzione è corretta, è attualmente
impossibile trovarla con un algoritmo deterministico, come quello sopra
riportato, anche ricorrendo all’ausilio dei più potenti computer[6]. In pratica questi problemi si risolvono
ricorrendo ad algoritmi non deterministici. Nel caso del problema in questione
si ha un algoritmo di questo tipo considerando al passo 1, invece dell’insieme di tutti i cammini
attraverso il grafo, un insieme di cammini generato casualmente. Quest’ultimo algoritmo viene
solitamente eseguito con l’ausilio di un calcolatore elettronico, Leonard
Adleman ne ha invece escogitato una realizzazione che usa come oggetti di
calcolo frammenti di DNA e come operatori particolari enzimi e tecniche di
biologia molecolare. Egli ha poi attuato l’algoritmo nel caso di un grafo con 7
vertici e 14 lati, vedi Fig. 4.
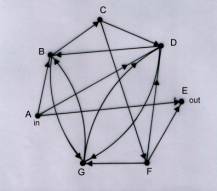Fig. 4
La prima descrizione dell’esperimento fu fatta dall’autore in un articolo
pubblicato su Science il 18 aprile
1994, [1]. Qualche anno dopo egli ne ha fornito anche una esposizione
divulgativa apparsa su Scientific American, [2].
Per la sua realizzazione in primo luogo si associa ad
ogni vertice un filamento di una sequenza casuale di DNA della lunghezza di 20
nucleotidi. Tale sequenza è rappresentata da 20 lettere scelte nell’insieme {A,
T, G, C}. Ogni lato orientato del grafo viene invece codificato da un filamento
di DNA in cui la sequenza dei nucleotidi è formata con la seconda metà della
sequenza che identifica il primo vertice e la prima metà di quella del secondo vertice.
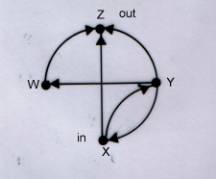Fig.5
Per semplicità di esposizione descriviamo il
procedimento facendo riferimento ad un grafo con quattro vertici X, Y, Z, W e
un cammino di sei lati, vedi Fig.
5, nel quale si vuole determinare l’esistenza di un percorso hamiltoniano che
inizia nel vertice X e termina nel vertice Z. Inoltre codifichiamo i vertici e
i lati con sequenze di soli 8 nucleotidi. Per motivi che saranno chiariti in
seguito accanto al codice di ogni vertice scriviamo anche il suo complemento
ricordando che le coppie di basi complementari sono, {A,T }, {G,C}.
|
Vertice |
Codice DNA |
Complemento |
|
X |
ACTTGCAG |
TGAACGTC |
|
Y |
TCGGACTG |
AGCCTGAC |
|
Z |
CCGAGCAA |
GGCTCGTT |
|
W |
GGCTATGT |
CCGATACA |
I lati
del grafo risulteranno quindi codificati nel modo seguente
|
Lati |
Codice DNA |
|
XY |
GCAGTCGG |
|
XZ |
GCAGCCGA |
|
YW |
ACTGGGCT |
|
YZ |
ACTGCCGA |
|
YX |
ACTGACTT |
|
WZ |
ATGTCCGA |
Codificati i nomi dei vertici e dei lati si
sintetizzano filamenti di DNA corrispondenti ai codici dei lati e ai
complementari dei codici dei vertici.
Il passo 1 dell’algoritmo viene realizzato
mettendo in una provetta un numero sufficientemente grande di filamenti di ciascuno
dei DNA sintetizzati assieme ad acqua, all’enzima ligasi, sali ed altre
sostanze che favoriscano il processo biologico dell’accoppiamento[7].
In questo modo si formano pressoché istantaneamente (quasi) tutti i possibili
cammini tra i vertici.
Il procedimento con cui questo avviene è il seguente.
Quando per esempio i filamenti di DNA che codificano il lato XY, GCAGTCGG, e il
nome complementare del vertice Y, AGCCTGAC, si incontrano, poiché la seconda
parte della prima sequenza, TCGG,
è complementare alla prima parte della seconda, AGCC, le due estremità
si appaiano, vedi Fig. 6.
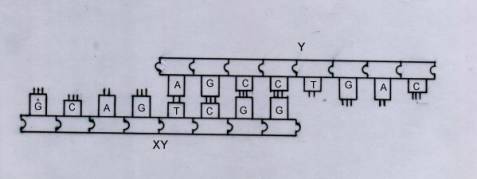
Fig. 6
Se il filamento ACTGGGCT che codifica il lato YW
incontra la molecola di Fig. 6 si unirà ad essa, poiché la sua parte iniziale
ACTG è complementare di TGAC parte finale di Y, vedi Fig. 7.
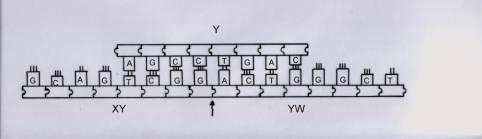
Fig. 7
In questo modo si formano catene che codificano i lati
e sono tenute insieme dai DNA complementari dei vertici. Questi legami sono
resi stabili dall’enzima ligasi presente nella soluzione. Nella provetta quindi
si formano molecole di DNA che codificano percorsi casuali attraverso i vertici
del grafo, così come richiesto dal
passo 1 dell’algoritmo. Tenuto conto del numero assai grande di
molecole messe in gioco è verosimile che si siano formati (quasi) tutti i cammini
possibili e che quindi almeno una delle molecole presenti nella provetta
codifichi l’eventuale percorso hamiltoniano.
La provetta dopo questa prima operazione contiene la
risoluzione, i passi successivi sono volti alla sua identificazione, cioè alla sua
estrazione dalla massa di molecole codificanti cammini, che si sono formate
assieme a lei.
Per realizzare il passo 2 dell’algoritmo, il
cui risultato finale è quello di scartare tutti i percorsi che non iniziano e
terminano nei vertici desiderati, si procede ricorrendo alla polimerasi,
eseguita in modo da amplificare esponenzialmente solo la duplicazione delle
sequenze che possiedono il corretto vertice di partenza e di arrivo.
Il passo 3 è reso operativo dall’elettroforesi
su gel che permette di separare tutte le molecole di DNA che hanno la lunghezza
giusta: 24 nel caso del nostro esempio, dove il cammino hamiltoniano deve
risultare lungo 3 ed ogni lato è codificato da 8 lettere; 120 nel caso
dell’esperimento eseguito da Adleman in cui il cammino hamiltoniano deve essere
lungo 6 ed ogni lato è codificato da 20 lettere.
Il passo 4 che prevede l’eliminazione dei
percorsi che non passano per tutti i vertici, viene realizzato usando
iterativamente la separazione per affinità, che sfrutta il principio di complementarietà
delle basi, e mediante il quale partendo dalla codifica di un vertice si
separano tutte le sequenze che contengono quel vertice. Queste vengono
trasferite in una nuova provetta dove si separano tutte le sequenze che
contengono un vertice diverso dal precedente e si trasferiscono. E’ chiaro che
dopo aver effettuato il procedimento per ogni vertice del grafo, le eventuali
molecole di DNA che rimangono passano per tutti i vertici una ed una sola
volta. Questo è il passo che sperimentalmente risulta più lungo e complicato.
Il passo 5 volto alla verifica della presenza
nella provetta di almeno una molecola di DNA, viene effettuato amplificando il
risultato del passo 4 con una polimerasi, seguita da un elettroforesi su gel
che permette di identificare l’eventuale molecola di DNA presente e quindi di
descrivere il percorso hamiltoniano da essa codificato. Nel caso del nostro
esempio si dovrebbe ottenere la sequenza GCAGTCGGACTGGGCTATGTCCGA, che codifica
il cammino (XY)(YW)(WZ).
Adleman alla fine di una settimana passata in
laboratorio per risolvere il problema relativo al grafo della Fig. 4, ebbe in
effetti la soddisfazione di trovare la soluzione.
Il lettore che ci ha seguito fin qui e che sicuramente
ha risolto il PPHO per il grafo della Fig. 4 in meno di un minuto, si starà
certamente domandando se valeva la pena di stare una settimana in laboratorio
ad eseguire tante noiose operazioni per ottenere un risultato così semplice.
L’autore stesso dell’esperimento che, ricordiamo, è anche un matematico e un
informatico di grande valore, risponde a questa domanda mettendo in evidenza
che il suo scopo non era tanto quello di risolvere quell’istanza, peraltro
banale del problema, bensì quello di dimostrare la possibilità di calcolare
con il DNA.
Egli, infatti, intravedeva in questo nuovo metodo
accanto ad evidenti svantaggi, quali la lunghezza delle operazioni biologiche,
la possibilità di errori nella loro esecuzione, che con il tempo si sarebbero
potuti in gran parte eliminare od attenuare, non pochi aspetti positivi. “Primo
fra tutti, quello di poter memorizzare le informazioni con altissima densità.
Per esempio un solo grammo di DNA secco
che occupa un volume di circa un centimetro cubo, può immagazzinare le
informazioni contenute in circa mille miliardi di CD. Inoltre i computer a DNA
offrono un’ enorme capacità di calcolo parallelo”[8],
cioè di eseguire un grande numero di operazioni contemporaneamente, che nel
caso in questione si manifesta nella velocità con cui all’inizio della
procedura si realizzano i legami fra i vari segmenti di DNA che rappresentano i
possibili cammini attraverso il grafo. Adleman sottolinea anche la migliore
efficienza energetica dei computer molecolari rispetto a quelli elettronici.
Egli conclude il suo articolo divulgativo, [2], con la seguente affermazione:
“Negli ultimi cinquant’anni l’informatica e la biologia hanno conosciuto uno
sviluppo fiorente, e non c’è alcun dubbio che queste scienze avranno un ruolo
centrale nei progressi economici e scientifici del nuovo millennio. Ma biologia
e informatica, vita e computer sono legati fra loro. Sono sicuro che a chi
vorrà esplorali, l’incontro fra questi due campi del sapere riserverà grandi
sorprese”.
L’esperimento di Adleman suscitò grande interesse
anche fuori della comunità scientifica, esso infatti fu immediatamente
pubblicizzato dai più importanti quotidiani e riviste di divulgazione
scientifica statunitensi. In particolare il Discover Magazine nel suo numero di aprile del 1995 ha proposto una
chiara e interessante versione a fumetti dell’esperimento che si può leggere in
rete al seguente indirizzo http:/users.aol.com/ibrandt/discover_article.html.
Leonard
Adleman, nato il 31 dicembre 1945, è un figura di scienziato molto
interessante. Ha studiato all’Università della California, Berkeley, dove ha
conseguito il Bachelor in Matematica nel 1968 e il Ph.D. nel 1976. Dal 1976 al
1980 ha insegnato e fatto ricerca presso il Massachusetts Institute of
Technology. In questo periodo ha sviluppato, tra l’altro, assieme a Ronald Rivest
e Adi Shamir il sistema di crittografia a chiave pubblica denominato RSA dalle
iniziali dei cognomi dei suoi ideatori, che, nel 2002, hanno ricevuto per i
contributi forniti in questo campo il Turing Award, considerato il premio Nobel della Computer Science.
Fin dalla tesi di dottorato A. si è interessato degli aspetti teorico numerici
della complessità computazionale ottenendo nel corso degli anni notevoli
risultati sia nel campo della Theoretical Computer Science che in quello della
Teoria dei numeri. Nel 1993, allo scopo di poter meglio comunicare ai biologi
alcune sue scoperte sull’AIDS, iniziò a frequentare un laboratorio di biologia
molecolare dove si familiarizzò con le tecniche della biologia moderna[9].
A. affascinato dal DNA, in
particolare dalla sua capacità di immagazzinare e trasmettere informazioni, e
da alcuni processi biomolecolari,
pervenne all’idea di poter usare il DNA come strumento di calcolo. Fu così che
progettò ed eseguì personalmente l’esperimento sopra descritto. Da allora, pur
senza trascurare del tutto gli altri aspetti della sua attività scientifica, A.
si è dedicato costantemente allo sviluppo del calcolo con il DNA, fondando allo
scopo un “ Laboratory for Molecular Science” presso la University of South
California, Los Angeles, dove attualmente egli è sia professore di Computer
Science che di Molecular Biology.
3. Il Problema di soddisfacibilità per una formula
booleana
L’entusiasmo di Adleman verso il nuovo mezzo di
calcolo fu subito condiviso,
infatti poco dopo la pubblicazione del suo lavoro comparvero numerosi studi
sulle possibilità di risolvere altri problemi matematici con il DNA. Alcuni di
essi propongono strategie teoriche, altri descrivono invece la realizzazione
effettiva di algoritmi. Uno dei problemi che ha suscitato maggiore interesse è
quello della soddisfacibilità di una formula booleana, ( SAT-problem).
Una formula booleana (f.b.) è costruita a partire da un insieme finito di
variabili 
e dai connettivi
. Una f.b. 
si dice soddisfacibile se esiste almeno una sequenza di n valori scelti in 
per i quali essa
assume il valore 1. Nella interpretazione delle variabili solitamente si pensa
al valore 0 come “falso” e al valore 1 come “vero”; mentre 
corrisponde alla
congiunzione “oppure” (
sse 
), 
alla
congiunzione “e” (
sse 
), ’ viene
interpretato come “non” (x’=0 sse
x=1, x’=1 sse x=0). 
Per esempio 
è soddisfacibile
poiché
.
Il modo più naturale per verificare se una
f.b. è soddisfacibile è quello di
eseguire
il controllo per tutte le 2n possibili scelte per le n variabili. Al crescere del numero delle variabili e
della lunghezza della formula, la verifica diventa così lunga da superare la
capacità di calcolo di qualunque computer. Anche questo problema, infatti, è
stato classificato come NP-completo.
Un anno dopo la pubblicazione del lavoro di Adleman,
sempre su Science, apparve un articolo nel quale l’autore,
Richard Lipton, propone uno schema teorico di algoritmo per la risoluzione con il DNA del problema della
soddisfacibilità per una f.b. in forma normale disgiuntiva, [10]. Cioè per formule del tipo 
, dove ogni Bi
è una f.b. in cui
compaiono solo la congiuzione 
e variabili o
loro negazioni. Ciascuna delle Bi viene
detta clausola e se tutte le
clausole hanno la stessa lunghezza k,
cioè contengono tutte k variabili
o negazioni di variabili, si parla di k-formula, così la f.b. B(x,y)
sopra considerata è una 2-formula
con 2 clausole.
L’idea di Lipton per affrontare il problema è quella
di sfruttare la grande capacità di calcolo parallelo del DNA per generare
simultaneamente tutte le possibili assegnazioni di verità di una formula.
L’algoritmo che Lipton propone di realizzare con il DNA è il seguente:
Passo 0. Si generano tutte le possibili
assegnazioni di valori di verità per le variabili
Passo 1. Si eliminano tutte le assegnazioni che
non soddisfano la prima clausola.
Passo k+1. Si ripete il passo k
relativamente alla clausola k+1.
Passo m+1. Si verifica se sono rimaste
assegnazioni di valori di verità: In caso positivo si registra che il problema
ha soluzione.
Per la sua realizzazione in primo luogo si associa ad una qualunque
f.b. 
un grafo
orientato Gn aventi vertici a1,
x1, x’1, a2, x2, x’2 , …,an, xn, x’n,
an+1 e
lati che vanno da ai ad xi , xi’ e
da xi , xi ’ ad ai+1
, Fig. 8.
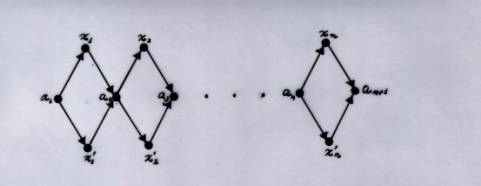
Fig. 8
I cammini che vanno da a1 ad an+1 si
possono prendere come codificazioni di un numero binario di n cifre. Ad ogni vertice ai , infatti, il cammino ha solo due scelte, se va verso
un vertice xi si conviene che codifichi 0, se va verso
un vertice x’i si conviene che codifichi 1.
Il grafo Gn viene poi codificato mediante filamenti casuali di DNA di 20
nucleotidi ciascuno con lo stesso sistema usato da Adleman nella risoluzione
del PPHO. Vale a dire ad ogni vertice Vi viena associata una sequenza di DNA piqi dove
pi, qi sono sequenze di 10 nucleotidi
ciascuna. Al lato ViVj
viene associata la sequenza q’ip’j dove
q’i , p’j
sono le sequenze complementari
di qi , pj..
All’inizio dell’esperimento si mettono in soluzione in
una provetta un numero sufficientemente grande di copie di filamenti di DNA che
codificano i vertici e i lati di Gn e copie di q’1 e
p’ n . Con il medesimo procedimento descritto nel caso
precedente si formeranno, per accoppiamento, tutti i cammini attraverso il
grafo, , la presenza di q’1
e p’ n assicura la prevalenza di formazione di
cammini da a1 ad an+1 . La struttura simmetrica del grafo assicura inoltre
che questi cammini si formeranno nella medesima quantità.
Per implementare gli altri passi dell’algoritmo, cioè
per verificare l’esistenza di un cammino che rappresenta la soluzione, Lipton
ricorre alla ripetizione di un’unica operazione biologica: l’estrazione. E(t,i,a) denota
l’insieme di tutte le sequenze presenti nella provetta t che hanno la componente i-esima uguale ad a con 
. E(t,i,a) si
determina con operazioni di estrazione per affinità. L’insieme delle sequenze
contenute nella provetta che non soddisfano alla condizione, viene detto resto.
L’algoritmo di risoluzione prevede la costruzione di
una successione di provette t0,t1,…,tm , la prima delle quali contiene tutte le n-sequenze a valori in 
, t1 contiene
solo le sequenze che soddisfano B1, t2 contiene le sequenze di t1 che soddisfano B2, etc.. Chiaramente tm conterrà solo le eventuali sequenze che soddisfano 
.
Per illustrare l’idea che guida la costruzione dei
passi successivi dell’algoritmo, per semplicità facciamo riferimento alla
formula 
il cui grafo G2
è formato dai vertici a1,
x, x’, a2, y, y’, a3. Tutti i cammini da a1 ad a3:
a1xa2ya3, a1xa2y’a3, a1x’a2ya3,
a1x’a2y’a3 , codificano rispettivamente le 2-sequenze : 00, 01, 10, 11, che
rappresentano tutte le possibili scelte di valori per le variabili di B(x,y).
Si tratta di costruire una
successione t0,t1,t2 di provette l’ultima delle quali conterrà solo le
eventuali sequenze di DNA che rappresentano le soluzioni.
Nella prima t0 ci sono
le sequenze 00, 01, 10, 11,
codificate da tutti i possibili cammini da a1 ad a3 sul grafo G2 associato
alla formula.
Passo
1. Sia τ1=E(t0,1,1), τ1 contiene le sequenze 10, 11, e il suo resto τ1’ le
sequenze 00, 01. Sia τ2= E(τ1’,2,1), τ2 contiene la sequenza 01. Allora 
contiene le
sequenze 01,10,11 che sono proprio quelle che soddisfano B1.
Passo
2. Sia τ3=
E(t1,1,0), τ3 contiene la sequenza 01 e τ’3 le sequenze 11, 10. Sia
τ
4= E(τ’3,2,0), τ4 contiene
la sequenza 10. Quindi 
contiene le sequenze 01, 10 che soddisfano anche B2.
Passo
3. Controllo della presenza di DNA nella provetta test di t2 e sua identificazione.
Nel caso generale di una formula 
con n variabili ed m clausole l’algoritmo risolutivo prevede la costruzione di una
successione di provette t0,t1,…,tm
tali che t0 contiene l’insieme di tutte le n-sequenze a valori in 
e tk il
sottoinsieme di quelle che soddisfano B1, B2, … , Bk.
Passo k+1-esimo. Supponiamo che sia stato costruita
tk , costruiamo tk+1. Sia 
dove ogni 
è una variabile
o la negazione di una variabile. Per ogni
si opera nel
modo seguente: se 
allora si
forma E(tk,j,1), se 
, allora si forma
E(tk,j,0). In
ogni caso per il calcolo relativo alla variabile successiva si usa il resto. Per formare tk+1 si mettono insieme tutte le provette ottenute in questo passo.
L’ultimo passo dell’algoritmo consiste nella
verifica della presenza di DNA nella provetta tm.
Si può notare che mentre la costruzione del grafo
iniziale e la preparazione della soluzione iniziale sono le stesse per tutte le
formule aventi lo stesso numero di variabili, l’algoritmo di selezione della
soluzione cambia al variare della formula. Osserviamo infine che i procedimenti
biologici implicati sono molto semplici: l’accoppiamento nella fase
iniziale e la estrazione per
affinità nell’esecuzione dei test E(
t,i,a).
Negli anni successivi alla pubblicazione dell’articolo di Lipton diversi
ricercatori hanno realizzato sperimentalmente il calcolo per alcune istanze del
problema di soddisfacibilità. Un succinto resoconto di alcune implementazioni
dell’algoritmo di Lipton ci permetterà anche di accennare a nuove tecniche
introdotte recentemente nel calcolo con il DNA.
Nel 2000 un gruppo guidato da L.M. Smith ha risolto
un’istanza del problema per una formula con quattro variabili, [11], impiegando
una nuova tecnica detta “chimica delle superfici solide”, in cui i filamenti di
DNA che codificano tutti le possibili assegnazioni di valori di verità alle
incognite vengono attaccati a un quadratino di vetro ricoperto da una lamina
d’oro. Successivamente ad essi vengono applicati enzimi di restrizione che
distruggono tutti quei filamenti di DNA che non soddisfano la formula booleana.
Sembra che questa tecnica delle superfici solide semplifichi notevolmente i
passi più complessi e ripetitivi dei primi calcoli con il DNA.
Sempre nello stesso anno K. Sakamoto e altri, [13],
hanno risolto un’istanza del problema per una 3-formula con sei variabili e
dieci clausole sfruttando la formazione di particolari strutture secondarie di
singoli filamenti di DNA, gli “hairpin”[10].
Una
implementazione per una formula con nove variabili collegata al ben noto
“Problema del cavallo” degli scacchi, è stata fornita da L.F. Landweber ed
altri, [7], usando una combinazione di tecniche di DNA e RNA.
Il risultato più importante finora ottenuto riguarda
una 3-formula con 20 variabili e 24 clausole avente una sola assegnazione di
valori che la soddisfa, [4]. Il procedimento usato da Adleman e dai suoi
collaboratori usa l’ibridazione di brevi filamenti di DNA detti
“sticker”(etichetta) per codificare le assegnazioni di valori di verità delle
20 variabili booleane. Il calcolo successivo è reso possibile dall’uso di una elettroforesi su gel
automatizzata che estrae i filamenti di DNA che hanno “sticker” che codificano
assegnazioni delle variabili che soddisfano la formula booleana.
Sebbene
il calcolo sia stato eseguito per una formula avente una particolare struttura
iterativa, in nessun passo si è fatto uso di essa, pertanto gli autori
ritengono che il loro procedimento possa testare una qualunque 3-f.b. con 20
variabili e 24 clausole. Essi ipotizzano anche la sua utilizzazione per formule
fino a 30 variabili.
L’importanza di quest’ultimo calcolo risiede anche
nella circostanza che la verifica della soddisfacibilità della formula in
questione richiede l’esame di 220= 1.018.576 possibilità di
assegnazione di valori di verità. Verifica che ovviamente può essere fatta con
un computer elettronico, ma che certamente non può essere fatta a mano come nel
caso dell’istanza del PPHO risolta da Adleman.
4.
Commenti e ulteriori prospettive
Nei dieci anni trascorsi dalla comparsa del
fondamentale articolo di Adleman il settore del calcolo con il DNA ha
conosciuto una notevole evoluzione testimoniata dai numerosi convegni ad esso
dedicati e dalla
moltitudine di pubblicazioni apparse sull’argomento[11].
Tra i problemi, oltre a quelli che abbiamo presentato, per i quali sono stati
proposti o effettivamente eseguiti algoritmi, ricordiamo: la decrittazione del
codice DES, l’espansione simbolica di determinanti, la colorazione di grafi e
tentativi di realizzazione di un’aritmetica binaria.
Ampio spazio è stato riservato anche ai dibattiti
sugli aspetti che renderebbero i DNA-computer più convenienti rispetto a quelli
elettronici attualmente in uso. A favore dei primi vengono messe in risalto le
notevoli capacità di calcolo parallelo e il basso consumo energetico. Per
quanto riguarda quest’ultimo fattore ricordiamo che recentemente alcuni
ricercatori del Weizmann Institute of Science a Rehovot (Israele), hanno
eseguito un calcolo con il DNA a costo energetico zero, [3]. Relativamente al
primo aspetto si deve invece sottolineare che, sebbene il massiccio
parallelismo del calcolo con il DNA permetta teoricamente di eseguire tutti gli
algoritmi in tempo polinomiale, sfortunatamente la loro applicabilità è
limitata a piccole istanze, infatti, mentre gli algoritmi hanno tempo di
esecuzione lineare nelle dimensioni degli input, la massa di DNA necessario per
le codificazioni cresce esponenzialmente. Per esempio è stato calcolato che il
DNA necessario per codificare tutti i cammini di un grafo con 200 vertici
avrebbe una massa pari a quella della terra. L’algoritmo di Adleman per il PPHO
potrebbe essere realizzato per un grafo avente al massimo 70 vertici, ma in tal
caso il calcolo può essere eseguito in modo più conveniente con i computer
elettronici, i quali attualmente possono gestire grafi con un numero molto
maggiore di vertici.
Altri argomenti a sfavore dei DNA-computer sono la
possibilità di errori dovuti sia alla esecuzione pratica delle operazioni
biologiche con le quali si realizza l’algoritmo, che alle codificazioni, le
quali se non sono sufficientemente accurate potrebbero permettere, nella fase
iniziale, la formazione di sequenze di DNA non previste. A questi errori si può
comunque ovviare più facilmente. Le tecniche di biologia molecolare si stanno
evolvendo rapidamente e molte delle operazioni necessarie per il calcolo vengono
ora eseguite automaticamente limitando in tal modo la possibilità di errori.
Allo stato attuale delle conoscenze, nonostante
l’estremo interesse degli esperimenti già effettuati, manca un’esempio “cruciale”, cioè un calcolo che si possa
eseguire più vantaggiosamente con un DNA computer. Questo non toglie validità
alle ricerche fatte finora e stimoli alle ricerche future sui cui risultati gli
autori di [4], fra i quali figura
anche Adleman, sono molto fiduciosi. Nella conclusione del loro articolo infatti
affermano: “Nonostante i nostri successi e quelli di altri, in assenza di una
scoperta tecnica decisiva, l’ottimismo circa la creazione di un computer
molecolare capace di competere con i computer elettronici sui classici problemi
computazionali non è garantita. Comunque i computer molecolari possono essere
considerati in un contesto più ampio. Possono essere utili in particolari
circostanze nelle quali, per esempio, sia richiesta una estrema efficienza
energetica e una notevole densità di informazione. Possono fornire un mezzo
molto richiesto per controllare sistemi chimici/biologici nello stesso modo in
cui i computer elettronici hanno fornito un sistema per controllare sistemi
elettrici/meccanici. … Essi ci forniscono qualche idea su alternative ai computer
elettronici e studiandoli potremmo alla fine pervenire al vero “computer del
futuro”. Quel che più conta, i DNA computer , … , mostrano che le molecole
biologiche possono essere usate per scopi decisamente non biologici. Per tali
scopi queste molecole rappresentano un’eredità non utilizzata di 3 miliardi di
anni di evoluzione, e c’è un grande potenziale nella loro futura esplorazione”.
Forse gli scienziati in questione possono sembrare
troppo ottimisti, è comunque necessario ricordare che in presenza di un nutrito
pacchetto di problemi NP-completi, rispetto ai quali i computer elettronici sono impotenti, già da un paio di
decenni gli scienziati stanno cercando macchine di calcolo alternative e in
questa prospettiva anche i DNA computer presentano caratteristiche
interessanti.
Alcuni ricercatori ipotizzano perfino che si possano
costruire macchine ibride che usino i tradizionali chip al silicone per i
procedimenti normali ma con co-processori al DNA che portino a termine compiti
più adatti per loro.
Bibliografia
1.
L.A. Adleman, Molecular Computations of Solutions to Combinatorial
Problems, Science, 18 april 1994, 1021-1024
2.
L.A. Adleman, Computing with DNA, Scientific American, August
1998, 54-61, Trad. It. In “Le Scienze”, Ott. 1998.
3.
Y. Benenson, R. Adar, T. Paz-Elizur, Z. Livneh, E. Shapiro, DNA molecule provides a computing
machine with both data and fuel, Proc. Nat. Acad.
Sci. USA, 2003
4.
R.S. Braich, N. Chelyapov, C. Johnson, P.W. Rothemund, L. Adleman, Solution
of a 20-variables 3-SAT Problem on a DNA computer, Science, 28 April 2002,
499-502.
5.
F. Capitelli, F. Iozzi, DNA,
ultima frontiera del calcolo?,
Lettera Matematica, 27-28, 1998, 14-19.
6.
D. Fallis, Mathematical proof and the reliability of DNA evidence, Am.Math. Monthly,
103(6), 1996, 491-497.
7.
D. Faulhammer, A.R. Cukras, R.J. Lipton, L.F. Landweber, Molecular
computation: RNA solution to chess problem, Proc. Nat. Acad. Sci.
USA, 97 (2000), 1369-1395.
8.
D.K. Gifford, On the Path to Computation with DNA, Science, 266, 11
nov. 1994, 993-994.
9.
L. Kari, DNA Computing: Arrival of Biological Mathematics, Mathematical
Intelligencer, 19(2), 1997, 9-22.
10.
R.J. Lipton, DNA Solution of hard Computational Problems, Science, 28 April
1995, 542-545.
11.
Q. Liu, L. Wang, A.G. Frutos, A.E. Condon, R.M. Corn, L.M. Smith, DNA
computing on surfaces, Nature, 403, 2000.
12.
J.H. Reif, Success and Challenges, Science, 19 April 2002,
478-479.
13.
K. Sakamoto, H. Gounzu,
K.Komiya, D. Kiga, S. Yokoyama, T. Yokomori, M. Hagiya, Molecular
computation by DNA hairpin formation, Science, May 19, 2000,
1223-1226.
NOTA.
Questa è una prima versione, il testo definitivo sarà stampato sul Bollettino
dell’UMI sez.A. Ogni osservazione e correzione volta a migliorare il testo è
benvenuta.